출처: https://sacko.tistory.com/10?category=632408
퍼셉트론 Perceptron
문과생도 이해하는 딥러닝 (1)
딥러닝이라는 말이 학계, 업계 어디든 할 것 없이 엄청난 화두이다. 그래도 아직까지는 기계학습이면 충분하지만 점점 더 인공지능과 관련된 신경망 기반의 딥러닝 알고리즘들에 대한 수요가 더욱 중요해질 것이다.(그것이 설령 필요하지 않더라도... 오버스펙...) 어쨌든 기계학습(machine learning) 알고리즘의 하나일 뿐인 딥러닝이 이제는 기계학습이라는 용어 자체를 대변하려는 기세를 보이고 있다. 기계학습에 대해 설명한 좋은 글들이 많이 있다. 간단하게 본다면 기계학습은 기계가 학습하는 것이다!(?) 컴퓨터는 인간에 비해서 복잡한 연산을 아주 빠르게 소화할 수 있는 기계일 뿐이었고 사람과 같이 무언가를 인식하는 것은 하지 못했다. 기계학습은 기계가 학습을 해서 인간처럼 사물도 인식하고 무언가를 분류해보고 묶어보고 하도록 하는 것이라고 보면 된다.
최근 기존 기계학습 방식으로는 처리가 어려운 문제를 딥러닝으로 해결해보려는 시도가 많아지고 있는 만큼 아직 기계학습(머신러닝)을 살펴보는 중이지만 딥러닝에 대해서도 본격적인 공부를 해보려고 한다.
1. 퍼셉트론 기초 개념
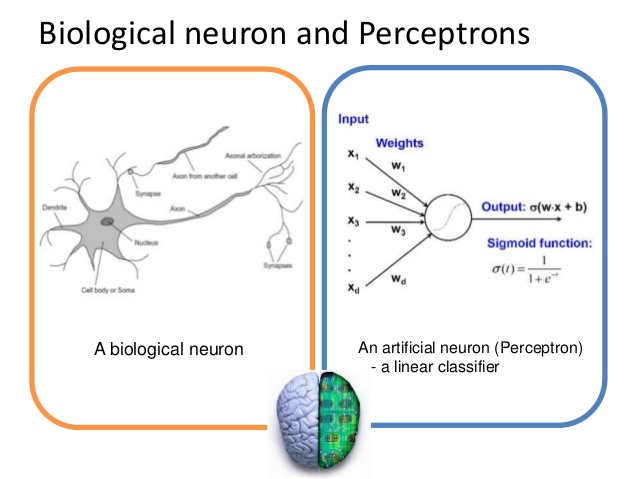
인공 신경망 모형의 하나인 퍼셉트론은 1957년에 Rosenblatt라는 사람에 의해서 처음 고안된 아주 오래된? 알고리즘이다. 일반적으로 인공 신경망 시스템은 동물의 신경계를 본따 만들었기 때문에 개념적으로나 그 형태로나 비슷한 부분이 많다. 아래 왼쪽의 뉴런(neuron) 그림은 생물을 공부해본 사람들은 모두 한 번쯤은 봤을 것이다. 생물심리학을 공부할 때 또 봤다...

퍼셉트론은 다수의 신호(Input)을 입력받아서 하나의 신호(Output)을 출력한다 이는 뉴런이 전기신호를 내보내 정보를 전달하는 것과 비슷해 보인다. 그리고 뉴런의 수상돌기나 축색돌기처럼 신호를 전달하는 역할을(정확한 말은 아니고 편의상 이렇게 설명... 용어가 아직도 기억이 나다니...) 퍼셉트론에서는 weight가 그 역할을 한다. 가중치라고 부르는 이 weight는 각각의 입력신호에 부여되어 입력신호와의 계산을 하고 신호의 총합이 정해진 임계값(θ; theta,세타)을 넘었을 때 1을 출력한다. (이를 뉴련의 활성화activation 으로도 표현) 넘지 못하면 0 또는 -1을 출력한다.
각 입력신호에는 고유한 weight가 부여되며 weight가 클수록 해당 신호가 중요하다고 볼 수 있다.
여기서 기계학습이 하는 일은 이 weight(입력을 조절하니 매개변수로도 볼 수 있음)의 값을 정하는 작업이라고 할 수 있다.학습 알고리즘에 따라 방식이 다를 뿐 이 weight를 만들어내는 것이 학습이라는 차원에서는 모두 같다고 할 수 있다.

퍼셉트론의 출력 값은 앞에서 말했듯이 1 또는 0(or -1)이기 때문에 선형 분류(linear classifier) 모형이라고도 볼 수 있다. 보통 실수형의 입력 벡터를 받아 이들의 선형조합을 계산하는 것이며 다른 포스팅에서 다룬 벡터의 내적과도 유사하다. 선형 분류는 저 아래 그림에서 어떤 것인지 보면 알 수 있는데 간단하게 설명하면 초등학교 때 옆에 앉은 짝꿍과 티격태격하다 책상 중간에 선을 쫙 긋고 "이 선을 넘으면 다 내거"라고 했던 기억이 한번쯤은 있을지도 모르겠다. 선형 분류는 이와 비슷하게 평면 상에 선을 쫙 그어서 여기 넘으면 A, 못 넘으면 B 이런식으로 분류하는 것이다.
2. 퍼셉트론 학습 방법
처음에는 임의로 설정된 weight로 시작한다.
학습 데이터를 퍼셉트론 모형에 입력하며 분류가 잘못됐을 때 weight를 개선해 나간다.
weight를 개선해 나간다는 의미는 우리가 수학 문제를 잘못 풀었을 때 선생님이 다시 풀어오라고 하면 정답에 맞게 풀기 위해서 다시 풀고 다시 풀고 하다가 정답을 맞추는 것과 비슷하다. 그래서 학습이라고 부른다. 이 학습이라는 말이 실제 우리가 생각하는 학습의 개념과 유사한 점이 많아 학습 심리학에서 공부했던 내용을 추후에 접목해서 따로 소개하고자 한다.

출처: https://www.slideshare.net/Nicolas_Nicolov/machine-learning-14528792
퍼셉트론은 모든 학습 데이터를 정확히 분류시킬 때까지 학습이 진행되기 때문에 학습 데이터가 선형적으로 분리될 수 있을 때 적합한 알고리즘이다. 이와 관련된 퍼셉트론 모형이 가지는 한계는 후에 설명하겠다. 선형분류는 아래와 같이 선으로 분류하는 것을 의미한다. 학습이 반복될수록 선의 기울기가 달라지는 것을 볼 수 있다. 학습을 하면서 weight가 계속 조정(adjust)되는 것이다.

출처: https://en.wikipedia.org/wiki/Perceptron
3. 가중치와 편향
앞의 퍼셉트론 수식에서 나오는 세타θ를 -b로 치환하여 좌변으로 넘기면
b + w1x1 + w2x2 <0 => 0
b + w1x1 + w2x2 >=0 => 1
과 같이 되며 여기에서 b를 편향(bias)라고 할 수 있다. 기계학습 분야에서는 모델이 학습 데이터에 과적합(overfitting)되는 것을 방지하는 것이 중요하다. 여기서 과적합이라 함은 모델이 엄청 유연해서 학습 데이터는 귀신같이 잘 분류하지만, 다른 데이터를 넣어봤을 때는 제대로 성능을 발휘하지 못하는 것을 말한다. 어느 데이터를 넣어도 일반적으로 잘 들어맞는 모델을 만드는 것이 중요하다.
따라서 앞에서 설명했듯이 편향은 θ(theta)로 학습 데이터(Input)이 가중치와 계산되어 넘어야 하는 임계점으로 이 값이 높으면 높을 수록 그만큼 분류의 기준이 엄격하다는 것을 의미한다. 그래서 편향이 높을 수록 모델이 간단해지는 경향이 있으며 (변수가 적고 더 일반화 되는 경우) 오히려 과소적합(underfitting)의 위험이 발생하게 된다. 반대로 편향이 낮을수록 한계점이 낮아 데이터의 허용범위가 넓어지는 만큼 학습 데이터에만 잘 들어맞는 모델이 만들어질 수 있으며 모델이 더욱 복잡해질 것이다. 허용범위가 넓어지는 만큼 필요 없는 노이즈가 포함될 가능성도 높다. 이를 편향과 분산의 트레이드오프 관계라고 보통 부르며 기회가 되면 이 부분을 더 다뤄보도록 하겠다. (포스팅 추가)
쉽게 예를 들어 '다문화'와 연결해서도 생각해 볼 수 있을 것 같다. 정확한 의미는 다르지만 유럽에서는 경제성장을 위해서 다국적의 사람들의 이민을 쉽게 허용해주었고 그들의 고급 노동력뿐만 아니라 그 아래 노동력도 포함해서 많은 인력을 수급하였다. 그 결과 경제성장의 밑거름이 되었다. ( + ; 학습한 모델이 잘 들어맞는 상황) 하지만, 다문화의 차이로 인한 갈등, 범죄율 상승 등의 문제가 발생하였다. ( - 손해; overfitting) 그렇다고 이민정책을 엄격하게 잡으면 사람들을 적게 받아 큰 플러스 효과를 보지 못할 수 있다. (- 손해; underfitting)
위의 예시는 적절하다고 볼 수는 없으나 결국 그 핵심은 학습의 과정에서 불순물(Noise)가 얼마나 포함되고 이것을 잘 걸러내줄 수 있느냐가 관건임을 말하고 싶었던 것이다.
요약하면, 가중치(weight)는 입력신호가 결과 출력에 주는 영향도를 조절하는 매개변수이고, 편향(bias)은 뉴런(또는 노드; x를 의미)이 얼마나 쉽게 활성화(1로 출력; activation)되느냐를 조정하는(adjust) 매개변수이다.
4. 퍼셉트론의 한계점
하지만 퍼셉트론이 인공지능 분야에서 센세이션을 불러일으켰고 연구 과제도 이쪽으로 몰렸으나 이것이 가지는 한계점이 밝혀지면서 한동안 소외 받는 이론이 되었다. 퍼셉트론을 제시한 로젠블랫은 자살 같은 사고로 세상을 떠났고 시간이 흐른 뒤에야 그의 업적이 재조명 받았다. 퍼셉트론의 한계는 선형으로 분류를 할 수 있지만 XOR와 같이 선형 분류만 가능하며 비선형 분류는 불가능하다는 점이다.
XOR 논리는 exclusive(배타적) 논리연산이다. 아래의 진리표를 보면, x1과 x2 중 어느 한쪽이 1일 때만 1을 출력한다.
|
x1 |
x2 |
y |
|
0 |
0 |
0 |
|
1 |
0 |
1 |
|
0 |
1 |
1 |
|
1 |
1 |
0 |
아래의 그림을 보면 XOR에서는 선형으로(직선 하나로) 분류가 불가능함을 알 수 있습니다.

출처: http://ecee.colorado.edu/~ecen4831/lectures/NNet3.html
퍼셉트론의 한계를 간략히 말하면, 직선 하나로 나눈 영역만 표현할 수 있어 XOR과 같은 데이터 형태는 분류가 불가능하다는 한계가 있다.
5. 다층 퍼셉트론을 통한 한계 극복
단일 퍼셉트론으로는 XOR을 분류할 수 없지만, 다층 퍼셉트론을 만들면 이를 극복할 수 있습니다. 다층(multi-layer)이라는 말은 하나의 퍼셉트론에 또 다른 퍼셉트론을 덧붙인다는 의미로 볼 수 있다. 단층 퍼셉트론이 비선형 영역을 분리할 수 없다는 것이 문제이며 다층으로 할 경우 비선형으로 이를 해결할 수 있다.

출처: https://commons.wikimedia.org/wiki/File:Perceptron_XOR.jpg
이런식으로 층을 겹겹이 쌓아나가면서 선형 분류만으로는 풀지 못했던 문제를 비선형적으로 풀 수 있게 된다.
퍼셉트론의 알고리즘은 문과생도 바로 이해할 수 있었던 아주아주 쉬운 알고리즘이다. 신경망의 기초가 되므로 이번에 이해한 내용은 그 베이스로 중요하다고 할 수 있다.
'IT기술 관련 > A.I 인공지능' 카테고리의 다른 글
| 문과생도 이해하는 딥러닝 (2) - 신경망 Neural Network (0) | 2019.10.12 |
|---|---|
| 회귀분석 유형의 이해 (0) | 2019.10.11 |
| 문과생을 위한 딥러닝 수학 - 핵심편 (1) (0) | 2019.10.10 |
| 문과생을 위한 딥러닝 수학 - 기본편 (4) 절댓값 함수, 가우스 함수 (0) | 2019.10.09 |
| 범주형,수치형,이상형,연속형,명목형,순서형 정리 (0) | 2019.10.08 |