출처: https://sacko.tistory.com/40?category=630831
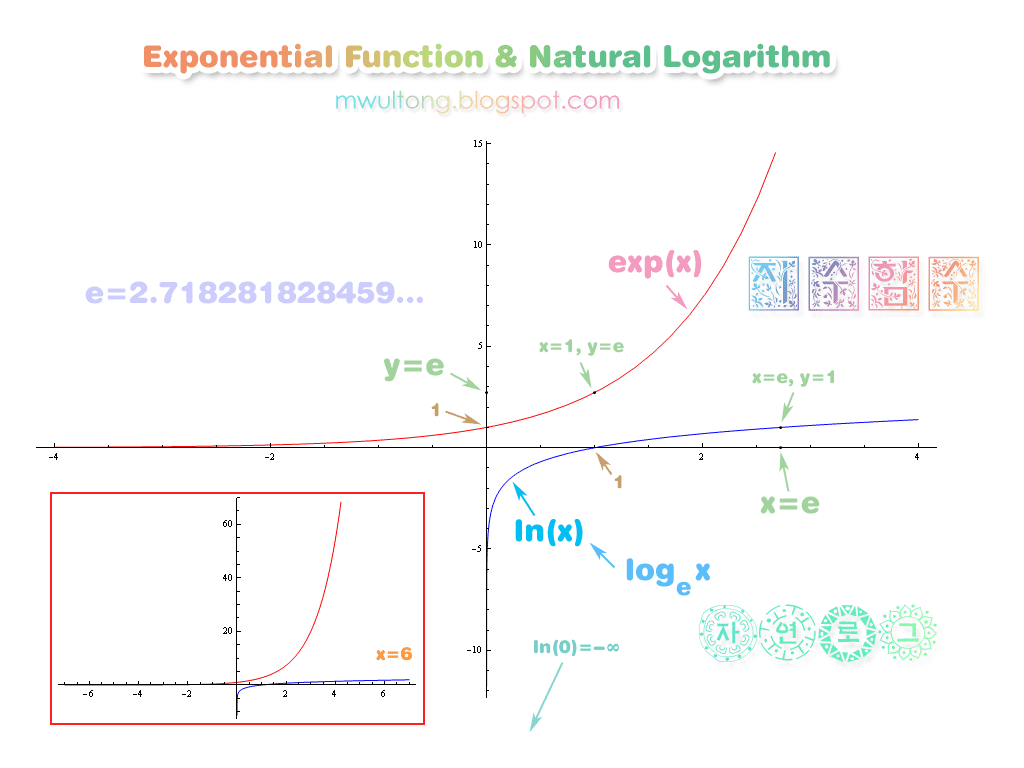
딥러닝 신경망 학습에서 시그모이드 함수(Sigmoid Function)를 활성화함수로 사용한다. 시그모이드 함수는 1/1+exp(-x) 로 나타나는데 여기서 exp(-x) exponential function으로 자연상수e(약2.71)에 대한 지수함수를 의미한다. exp(-2)일 경우 약 2.71의 제곱.. 시그모이드 함수의 사용 이유는 비선형적으로 출력값을 매끄럽게 하기 위한 것이며 자세한 내용은 지난 포스팅을 참고하면 된다.
왜 밑을 e인 자연로그함수를 사용하는가 하냐면 큰 수의 복잡한 계산을 할 때 계산을 단수화하기 위해서 사용된다. 특히 자연로그를 사용했을 때 미적분의 계산이 간편하다고 한다. 기울기를 계산하거나 오차역전파에 대한 계산을 할 때 미분을 사용한다.
자연로그(ln)의 역함수는 지수함수인 exp(x)이다.
문과생을 위한 딥러닝 수학 - 기본편 (2)
지수함수, 로그함수
3. 지수함수
1) 거듭제곱근 정의
실수 a와 2이상의 자연수 n에 대하여 n제곱하여 a가 되는 수를 말한다. 즉, 방정식 x제곱 = a를 만족시키는 수 x를 a의 n제곱근이라고 한다.
a의 제곱근, 세제곱근, 네제곱근, ...을 통틀어 a의 거듭제곱근이라 한다.
보통 말하는 루트a 를 말함.
2) x의 n제곱 = a 일 때의 거듭제곱근
- a>0 : n루트a, n루트a, -n루트a
- a=0 : 0
- a<0 : n루트a, 없음(제곱하여 음수가 나올 수 없음)
3) 거듭제곱근의 성질
출처: WINNER 수학
4) 지수법칙
대학미적분을 배우기 위해서 지수법칙을 하는 것이지만 지수법칙의 기본적인 공식은 숙지할 필요가 있음
출처: WINNER 교육전략
5) 지수함수
1이 아닌 양수 a일 때 임의의 실수 x에 대하여 a의 x제곱의 갑승ㄴ 단 하나로 정해지므로 y = a의x제곱
a가 1이면 어떤 실수 x를 대입해도 y 값이 1이 나옴
6) 지수함수 그래프

a>1 , x값이 증가할 때 y도 증가
0<a<1, x값이 증가할 때 y는 감소
x 축은 점근선(점에 가까워지는 선)이다 y=0에 가까워짐
그리고 항상 (0,1)을 지남
지수함수의 문제를 풀다보면 어느새 방정식, 부등식, 그래프 등에 대해서 풀고 있음.....
미분도 비슷하게 하다보면 방정식, 부등식, 그래프 등을 만지고 있을 듯 하다
지수함수의 x값을 f(x)로 본다면 먼저 f(x)를 풀이하고 지수함수로 돌아와서 다시 풀고 (Example 6 참조)
7) 지수함수 방정식과 부등식
4. 로그함수
1) 로그의 성질

2) 로그의 밑변환 공식

3) 상용로그의 지표와 가수
4) 로그함수 정의

5) 로그함수 y = logaX의 그래프

6) y = logaX 의 평행이동, 대칭이동
7) 로그방정식
'IT기술 관련 > A.I 인공지능' 카테고리의 다른 글
| 문과생을 위한 딥러닝 수학 - 기본편 (3) 유리함수, 무리함수 (0) | 2019.10.08 |
|---|---|
| 선형관계, 비선형관계, 단조관계 알아보자 (0) | 2019.10.07 |
| 독립변수 vs 종속변수 차이점을 알아보자 (0) | 2019.10.06 |
| 회귀분석(Regression) vs 상관분석(Correlation) 개념 차이 (0) | 2019.10.05 |
| 데이터 분석 vs 데이터 마이닝 개념 차이 (0) | 2019.10.04 |

